DINAMICA

1.  CONCEPTO:

La dinámica es la parte de la física que describe la evolución en el tiempo de un sistema físico en relación con las causas que provocan los cambios de estado físico y/o estado de movimiento. El objetivo de la dinámica es describir los factores capaces de producir alteraciones de un sistema físico, cuantificarlos y plantear ecuaciones de movimiento o ecuaciones de evolución para dicho sistema de operación.

El estudio de la dinámica es prominente en los sistemas mecánicos (clásicos, relativistas o cuánticos), pero también en la termodinámica y electrodinámica. En este artículo se describen los aspectos principales de la dinámica en sistemas mecánicos, y se reserva para otros artículos el estudio de la dinámica en sistemas no mecánicos.

En otros ámbitos científicos, como la economía o la biología, también es común hablar de dinámica en un sentido similar al de la física, para referirse a las características de la evolución a lo largo del tiempo del estado de un determinado sistema.

2.  HISTORIA:

La primera contribución importante se debe a Aristóteles. Aristóteles define, el movimiento, lo dinámico (το δυνατόν), como: "La realización acto, de una capacidad o posibilidad de ser potencia, en tanto que se está actualizando". El problema está en que Aristóteles invierte el estudio de la cinemática y dinámica, estudiando primero las causas del movimiento y después el movimiento de los cuerpos. Este error dificultó el avance en el conocimiento del fenómeno del movimiento hasta, en primera instancia, San Alberto Magno, que fue quien advirtió este error, y en última instancia hastaGalileo Galilei e Isaac Newton. De hecho, Thomas Bradwardine, en 1328, presentó en su De proportionibus velocitatum in motibus una ley matemática que enlazaba la velocidad con la proporción entre motivos a fuerzas de resistencia; su trabajo influyó la dinámica medieval durante dos siglos, pero, por lo que se ha llamado un accidente matemático en la definición de «acrecentar», su trabajo se descartó y no se le ha dio reconocimiento histórico en su día.¹

Ya con Galileo sus experimentos sobre cuerpos uniformemente acelerados condujeron a Newton a formular sus leyes fundamentales del movimiento, las cuales presentó en su obra principalPhilosophiae Naturalis Principia Mathematica Los científicos actuales consideran que las leyes que formuló Newton dan las respuestas correctas a la mayor parte de los problemas relativos a los cuerpos en movimiento, pero existen excepciones. En particular, las ecuaciones para describir el movimiento no son adecuadas cuando un cuerpo viaja a altas velocidades con respecto a la velocidad de la luz o cuando los objetos son de tamaño extremadamente pequeños comparables a los tamaños moleculares.

La comprensión de las leyes de la dinámica clásica le ha permitido al hombre determinar el valor, la dirección y el sentido de la fuerza que hay que aplicar para que se produzca un determinado movimiento o cambio en el cuerpo. Por ejemplo, para hacer que un cohete se aleje de la Tierra, hay que aplicar una determinada fuerza para vencer la fuerza de gravedad que lo atrae; de la misma manera, para que un mecanismo transporte una determinada carga hay que aplicarle la fuerza adecuada en el lugar adecuado.

3.  LEY FUNDAMENTAL DE LA DINAMICA

La segunda ley del movimiento de Newton se expresa así:

"El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime".⁶

Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en el momento lineal de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; esto es, las fuerzas son causas que producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre la causa y el efecto, esto es, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.

ECUACION: 

que es la ecuación fundamental de la dinámica, donde la constante de proporcionalidad, distinta para cada cuerpo, es su masa de inercia.

4.  VIDEO: 2° LEY  DE NEWTON:

5.  APLICACIONES -

5.1. EJERCICIOS  DE APLICACION RESUELTOS:

1.    A un cuerpo de masa m=10 Kg se le aplica una fuerza horizontal F=40 N si el coeficiente de rozamiento es μ=0,1 calcular:

a) La aceleración

b) La distancia recorrida a los 5 segundos.

R//

Datos: m = 10 kg

F = 40 N

µ = 0,1

 Aplicamos las ecuaciones dinámicas de movimiento:

a)    Hallemos a: Σ F_x = m.a_x                                       ΣF_y = m.a_y

F - f_r = 10 kg. a_x                                       N – W = 10 . 0

40 N - µ.N = 10 kg . a_x                      N – W = 0

40 N – 0.1.100 N = 10 kg.a_x                              N = W = m.g = 10kg. 10 m/seg²= 100 N

40 N - 10 N  = 10 kg . a_x

30 N   =  10 kg . a_x

     a_{x =} 30 N /10 kg

     a_{x =} 7,5 m/seg²      

b)    Hallemos x, al cabo de 5 seg: x = ½. a.t² = ½. (7,5). (5²)= 93,75 m

2.    Un ascensor de masa 8 toneladas está sometido a una aceleración dirigida hacia abajo de 1m/s². a) Calcular la tensión del cable que lo sostiene.

 

Datos: m (ascensor) = 8 tn = 8.000 kg

            a = 1 m/seg²

 

R// a) aplicamos suma de fuerzas en y por qué el movimiento es vertical:

 

 ΣF_y = m.a_y   luego: W– T = 8.000 kg. 1 m/seg²

 

mg −T = m. a

 

8000⋅ 9.8 −T = 8000(1)   luego: 78.400 – T = 8.000

T = 78.400- 8.000 = 70.400 N

3. Se arrastra un cuerpo de masa m= 25Kg por una mesa horizontal, con una fuerza F=80N que forma un ángulo de 60 grados y coeficiente de rozamiento μ=0,1 calcular:

a) aceleración

b) velocidad a los 3 segundos

 

Como la fuerza es diagonal y el cuerpo se mueve en forma horizontal, aplicamos:

Σ F_x = m.a_x       luego: F_x -  f_r =  m . a_x    y hallamos el valor de a_x :

F.cos 15° - µ.N = m .  a_x

80.( 0,96) – 0,1 N = 25 kg. a_x

76,8 – 0,1 . N = 25 . a_{x   (1)}

Hallemos el valor de N, con la ecuación:        ΣF_y = m.a_y   

Luego:  N – W = 0 entonces N = W =m.g = 25.(9.8) = 245 N    

Reemplazando e (1), tenemos:  76,8 – 0,1.(245) = 25 . a_x

Luego: 76,8 – 24,5 = 25. a_x,  entonces: 52,3 = 25 a_x

a_x = 52,3 /25 = 2,09 m/seg²

b) Hallemos ahora la velocidad al cabo de 3 seg:

v = a.t. + v₀ = 2,09 . 3 + 0 = 6,27 m/seg

5.3. PRACTICA DE  LABORATORIO " LEY FUNDAMENTAL DE LA DFINAMICA

NOMBRE: “LEY FUNDAMENTAL DE LA DINÁMICA”

1. OBJETIVO: Verificar la relación que existe entre la Fuerza aplicada sobre un cuerpo, su Masa y su respectiva  Aceleración.

2. MATERIALES:

·         Carro dinámico.

·         Juego de pesas de 0,5 N,1 N,2N ……5 N

·         Cuerda inextensible.

·         Una polea

·         Base soporte.

·         Prensa para mesa.

·         Varilla de 90 cm

·         Polea fija de 5 cm de radio

·         Juego de bloques de madera.

·         Cronometro.

·         Cinta métrica.

3. MONTAJE:

 

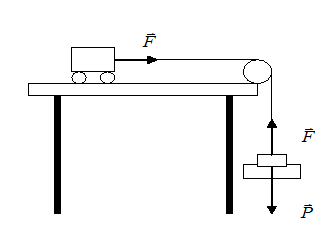
4. PROCEDIMIENTO:       Realice el montaje establecido y siga los   siguientes pasos:

A.  PRIMER CASO: Masa constante  y  Fuerza variable

Tome una distancia prudencial entre el carro y la polea y mida con el cronometro el tiempo que gasta el carro en recorrer esta distancia, variando la magnitud de las fuerza, desde 1 N hasta 5 N. Calcule la aceleración para cada caso y llene la siguiente tabla:

Tenga presente que si x = ½.a.t², entonces a = 2.x/ t²

 

TABLA N°1

N°	FUERZA (N)	TIEMPO (Seg)	ACELERACIÓN	F /  a
1	1 N
2	2 N
3	3 N
4	4 N
5	5 N

         ACTIVIDADES: Realice una gráfica de  Fuerza vs Aceleración, en un sistema de  

                   Coordenadas cartesianas y en papel milimetrado.

1.     ¿Qué clase de línea se obtiene?

2.     Si es recta calcule la pendiente respectiva, ¿Qué representa está pendiente?

3.     ¿Qué se puede concluir, respectó a la relación entre estas dos variables ( F y a  )?

B.  SEGUNDO CASO: Fuerza constante y Masa variable

Manteniendo constante la fuerza aplicada ( w = 5 N), varíe el valor de la masa del carro dinámico, con los bloques de madera.  Mida el tiempo que gasta en cada caso, en recorrer la distancia ya establecida y  calcule la aceleración del móvil.   Llene la siguiente tabla:

TABLA N°2

N	MASA (Kg)	TIEMPO(Seg)	ACELERACION	m . a
1
2
3
4

            ACTIVIDADES: Realice la gráfica de masa vs  aceleración en un sistema de

                   Coordenada cartesiana  en papel milimetrado y conteste:

1.     ¿Qué clase de grafica se obtiene?

2.     Halle  la constante que liga estas dos variables, realizando el producto de los valores de cada pareja ordenada.

3.     ¿Qué clase de relación elija estas dos variables?

4.     Realice un informe escrito y preséntelo, dentro de 8 días en la clase de física

                                                          DESARROLLO

5.4 . TALLER  DE APLICACION (VER TALLER DE DINAMICA)

NOTA:  Aplicando las ecuaciones dinámicas de movimiento, resuelva los siguientes ejercicios:

ΣF_x  =  m . a_{x         (ECUACIONES DINAMICAS)}

ΣF _y  =  m . a_y

TALLER N°13  DINÁMICA DE SÓLIDOS

1. Sobre una gran bascula esta un levantador de pesas con una barra de 90 kg.  Durante el proceso de subir y bajar la barra, ¿Qué variación podría sufrir la medida del peso que registraría la báscula?
2. Un  bloque se desliza por un plano inclinado  liso con una aceleración de 4,2 m/seg².  ¿Qué ángulo forma el plano con la horizontal?
3. De una cuerda que pasa a través de una polea  penden dos cuerpos de 100 kg y 240 kg.  Calcula la aceleración de los cuerpos y la tensión de la cuerda?
4. ¿Qué aceleración le imprime un plano inclinado 30°, a un cuerpo de 6kg que rueda sin rozamiento?. ¿Cuál seria la aceleración si existiera  rozamiento con un coeficiente de 0,25?
5. Dos masas de 8 kg, están ligadas por una cuerda  como lo indica la figura.  La mesa esta pulida y la polea no presenta rozamiento.  Calcula la aceleración del sistema y la tensión de la cuerda.  Fig. Nº1

6. Dos bloques de 5 kg y 3 kg se deslizan sobre planos inclinados  sin rozamiento.  Calcula la aceleración de las masas y la tensión de la cuerda.  Fig. N°2.
7. El coeficiente de rozamiento estático  entre un cuerpo de 6kg y una superficie horizontal  es de 0,2.  ¿Cuál es la fuerza horizontal máxima que se puede aplicar al cuerpo antes de que empiece a resbalar?
8. Un resorte se estira 2 cm cuando de el se suspende una masa de 24 kg.  Determine la deformación cuando se coloca el sistema  masa resorte,  sobre un plano inclinado sin rozamiento y que forma un ángulo de 42° con la horizontal.
9. Una persona de 58 kg, va en un automóvil a una velocidad de 65 km/h.  Si el auto describe un curva de 40 m de radio, ¿Cuál será la fuerza que ejerce la puerta del auto sobre la persona?
10. Dos bloques están unidos por una misma cuerda mediante unba ppoela fija sin rozamiento, si la masa del cuerpo 2 es de 12 kg, calcule el valor de la tensión del cable y la aceleración del, sistema.

                                                              DESARROLLO