El mundo de la fisica por ALONSO: agosto 2016

ESTÁTICA

CLASE 1.

La estática es la rama de la mecánica que analiza las cargas (fuerza, par / momento) y estudia el equilibrio de fuerzas en los sistemas físicos en equilibrio estático, es decir, en un estado en el que las posiciones relativas de los subsistemas no varían con el tiempo.
La estática se estudia amparados en La primera ley de Newton (Ley de la inercia), y se complementa con la tercera ley de newton (Ley de la acción y la reacción. Implica que la red de la fuerza y el par neto (también conocido como momento de fuerza) de cada organismo en el sistema es igual a cero. . La red de fuerzas de igual a cero se conoce como la primera condición de equilibrio, y el par neto igual a cero se conoce como la segunda condición de equilibrio.

1. CONCEPTO DE FUERZA:

Su palabra proviene del latín fortia. La fuerza es la capacidad para realizar un trabajo físico o un movimiento, así como también la potencia o esfuerzo para sostener un cuerpo o resistir un empuje.

Los efectos que puede tener una fuerza son que un cuerpo se deforme (por ejemplo, si apretamos o estiramos un trozo de goma de mascar); O que un cuerpo permanezca en reposo (por ejemplo, para mantener estirado un puente, hay que hacer fuerza sobre él),; lo que se conoce como efecto ESTATICO y que cambie su estado de movimiento (ya sea cuando el objeto este estático, o acelerarlo o frenarlo cuando se esté moviendo); conocido también como efecto DINÁMICO.

2. MEDIDA DE UNA FUERZA:

Para medir una fuerza se utilizan los dinamometros, que son instrumentos que funcionan gracias a la deformación de un resorte calibrado.

La unidad de mediada de una fuerza depende del sistema utilizado así.

Pondios o kilopondios: Sistema Ingles

Newtons: Sistema Internacional

K-fuerza: Sistema técnico

3. CLASIFICACIÓN DE LAS FUERZAS:

Para su estudio las fuerzas se pueden clasificar en dos clases, FUERZAS DE CONTACTO Y FUERZAS A DISTANCIA aunque en la naturaleza son muchas, pero la mayoría son de carácter gravitacional y electromagnético.

A. FUERZAS A DISTANCIA: Aquellas que actúan sin necesidad de tener contacto dirtrecto con el cuerpo, entre ellas tenemos:

1. FUERZAS GRAVITACIONALES: La fuerza ejercida por la Tierra sobre los objetos se denomina fuerza de gravedad. La gravedad es una de las fuerzas fundamentales de la naturaleza. Nadie realmente conoce exactamente porqué esta fuerza jala los objetos unos hacia los otros. La masa de los objetos y la distancia entre ellos afectan la magnitud de la fuerza gravitacional. A mayor masa de los objetos y a menor distancia entre ellos mayor es la intensidad de esa fuerza. Masas gigantes pueden atraer con mayor fuerza, mientras que a mayor separación las fuerzas se debilitan.

2. FUERZAS ELECTROMAGNÉTICAS: Se dividen en fuerzas eléctricas y magnéticas. Son aquellas que generan los cuerpos cargados electricamente, que actúan a distancia y pueden ser de atracción o de repulsión dependiendo del sentido de la carga.

3. FUERZAS NUCLEARES: Son aquellas que mantienen el átomo compacto, y no permiten que las partículas del núcleo salgan del el. Se dividen en nucleares fuertes y nucleares débiles.

B. FUERZAS DE CONTACTO: Entre ellas podemos enumerar:

1. FUERZA NORMAL: Es aquella que hace una superficie cuando un cuerpo se coloca sobre el. Es una fuerza de reacción al peso de un cuerpo.

2. FUERZA TENSORA:Es aquella que aparece como la reacción de una fuerza externa que se aplica sobre un cable o una cuerda, sujeta por el otro extremo:

3. FUERZAS ELÁSTICAS: Presentes en los cuerpos elásticos, como los resortes y fue definida por el científico Hooke, mediante la ley que lleva su nombre: LEY DE HOOKE, que se expresa como
F = - K. X. Donde F es la fuerza recuperadora del resorte, K es la constante de elasticidad del resorte y X es la deformación que sufre el resorte.

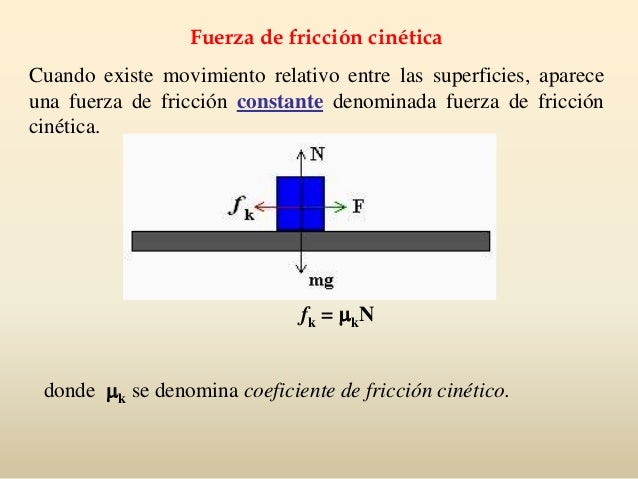
4. FUERZAS DE FRICCIÓN:Son aquellas que se presentan entre el cuerpo y la superficie, siempre se oponen al movimiento del cuerpo, y dependen del peso del cuerpo y de las características de la superficie M. se define como Fr < M.N.

CLASE 2:

4. LEYES DE NEWTON DE LA MECÁNICA:

1° LEY DE NEWTON: En ausencia de fuerzas externas un objeto en reposo permanecerá en reposo y un objeto en movimiento continuará en movimiento a velocidad constante (esto es, con rapidez constante en línea recta).

2° LEY DE NEWTON: la aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre él e inversamente proporcional a su masa.

De esta forma podemos relacionar la fuerza y la masa de un objeto con el siguiente enunciado:

3° LEY DE NEWTON: "Las fuerzas siempre ocurren en pares. Si el objeto A ejerce una fuerza F sobre el objeto B, entonces el objeto B ejerce una fuerza igual y opuesta -F sobre el objeto A"

RECOMENDACIÓN: Para mejor comprensión de como se observan las leyes de Newton en la vida diaria, puedes ver un video llamado: leyes de Newton explicados con ejemplos reales en youtube, en esta dirección: https://www.youtube.com/watch?v=zYmdw8AVDRg

CLASE 3: PRACTICA: LA LEYDE HOOKE. (ver guia de laboratorio)

CLASE 4: 5. EQUILIBRIO DEL CUERPO RIGIDO

4.1. EQUILIBRIO DE TRASLACIÓN: Cuando disponemos de un cuerpo en reposo o que se puede mover a velocidad constante, conforme a la primera ley de Newton:

"PRIMERA CONDICIÓN DE EQUILIBRIO"

Si un cuerpo esta en reposo o se mueve a velocidad constante, la sumatoria de la fuerzas que actúan sobre el se anulan y se escribe así:
∑ F = 0. luego ∑ Fx = 0. y ∑ Fy = 0.

EJERCICIO DE APLICACIÓN: Un cuerpo de 75 kg, lo sostienen dos cuerdas como lo muestra la figura. Calcule el valor de las fuerza que realiza cada una de las cuerdas: ( T 1 y T 2 )

Para la solución se deben seguir los siguientes pasos:
1. Realice un dibujo del problema.
2. Dibuje las fuerzas que actúan sobre el cuerpo.
3. Halle las componentes de cada una de las fuerzas presentes.
4. Aplique la primera condición de equilibrio.
5. Resuelva el sistema de ecuaciones lineales encontradas.

NOTA: DIAGRAMA DE CUERPO LIBRE:

Un diagrama de cuerpo libre, diagrama de cuerpo aislado o diagrama de fuerzas, es un esquema donde se representan mediante flechas a las fuerzas que actúan sobre un cuerpo.

Hay que asegurarse de incluir en el diagrama todas las fuerzas que actúan sobre el objeto, y como se trata de una magnitud vectorial, la flecha se encarga de señalar su dirección y su sentido, mientras que la longitud de la misma proporciona una idea del módulo o intensidad.

EJEMPLOS:

clase 4:

PROBLEMA DE APLICACIÓN:

Con base al modelo del ejemplo 1 de las gráficas anteriores, se plantea la siguiente situación:

"Un cuerpo de masa 75 kg, se suspende de tres cuerdas, que forman ángulos de 45°, 30° y 90°. hallar la fuerza de cada uno de los tensores: T1, T2 y T3.

R//

Nota: Como la masa del cuerpo es de 75 Kg, el peso del cuerpo W es de 750 N ( w = m.g).

DESARROLLO: (proceso)
1. Realizamos un dibujo. (ya esta). o un diagrama de cuerpo libre:
2. Ubiquemos las fuerzas presentes: T1, T2 y T3. Pero T3 = 75 kg . 10 m/seg2 = 750 nt. Luego solo faltan T1 y T2.

1. REALICEMOS UN DIAGRAMA DE CUERPO LIBRE:

2. Apliquemos la primera condición de equilibrio: (suma de fuerzas igual a cero)

ΣFx = T1x – T2x = 0 → T1x - T2x = 0 (1)

ΣFy = T2y + T2x = 0 → T2y + T1y – w = 0 (2)

Hallemos T2 y T1, Resolviendo el, sistema de ecuaciones: T1x - T2x = 0 (1)

T2y + T1y – w = 0 (2)

Trasformemos (1) asi: T1 cos 30° - T2 cos 45° = 0 → T1 (0,866) - T2 (0,70) = 0 y también (2)

T2y + T1y – w =0 → T2 sen 45° + T1 sen 30° = 750 N → T2 ( 0,70) + T1 (0,5) = 750 (2).

Luego, resolvamos el Sistema de ecuaciones por reducción, asi:

T1 (0,866) - T2 (0,70) = 0 (1)

T2 ( 0,70) + T1 (0,5) = 750___ (2)
Sumemos:

T1 (0,866) + T1 (0,5) = 750 → T1 (0,866 + 0,5 ) = 750 → T1 (1,366) = 750
→

T1 = 750 / 1,366 = 549

T1 = 549 N. Hallemos el valor de T2:

De T1 (0,866) - T2 (0,70) = 0 tenemos que T2 (0,70) = T1 (0,866) = 549 (0,70) = 475,43

Luego: T2 = 475,43/ 0,70 = 679,19 N; luego T2 = 679,19 N.

TALLER DE APLICACIÓN 1

Resolver los siguientes ejercicios:

1) Calcular para cada fuerza de la figura, F1, F2 y F3 , calcular:

a) sus componentes vectoriales: Vx , Vy

b) La sumatoria de sus componentes horizontales y verticales.

2) Un hombre de, empuja una carreta de 150 N, hacia arriba por un plano inclinado 20° sobre la horizontal. Determine:

El valor de la fuerza que realiza el hombre para que la carreta suba a velocidad constante por el plano inclinado.
El valor de la fuerza que realizaría el hombre, si existiera una fricción, con un coeficiente de 0.13.

Problema n° 3) Utilizando el método de descomposición rectangular, hallar la resultante y el ángulo que forma con la dirección positiva del eje X, de las siguientes fuerzas:

200 N en el eje X dirigida hacia la derecha
300 N, 60° por encima del eje X, hacia la derecha
100 N, 45° sobre el eje X, hacia la derecha
200 N en la dirección negativa del eje Y

Problema n° 4) Dos fuerzas F1 y F2 actúan sobre un punto, F1 es de 8 N y su dirección forma un ángulo de 60° por encima del eje X en el primer cuadrante, F2 es de 5 N y su dirección forma un ángulo de 53° por debajo del eje X en el cuarto cuadrante, determinar:

Las componentes de la resultante.
La magnitud de la resultante.
La magnitud de la diferencia F1 - F2

5) Dos hombres halan mediante una cuerda el bloque de la figura , con la fuerzas F1 y F2, sobre un plano horizontal.

¿Cuál es el valor de la fuerza resultante ejercida por ambos sobre el bloque? ( Utilice la expresión: (Fr²= F1²+ F2²+ 2. F1 . F2 . cos ϴ )
¿Qué dirección tendrá dicha fuerza?. (Calcule el ángulo con la expresión anterior. Teorema del coseno).

6) Un resorte sostiene un cuerpo de 200 kgf mediante un plano inclinado ( sin fricción) de 2,8 m de largo y 1,5 m de altura. ¿Cuál es el valor de la fuerza elástica aplicada por el resorte, para que el bloque no ruede por el plano?

7) El módulo de una F es de 20 N. La componente de la fuerza sobre el eje X es de 16 N. Entonces la componente sobre el eje Y vale? …

8) Cual debe ser el valor del peso que cuelga, si el peso del cuerpo en el plano inclinado es de 100N, para que el sistema este en equilibrio? (El coeficiente de fricción del plano es de 0,27)

9. Hallar el valor de las fuerzas de cada tensor de la figura.

DESARROLLO

CLASE 5:

4.2. EQUILIBRIO DE ROTACIÓN:

1. EFECTO ROTACIONAL: Podemos afirmar que un cuerpo esta en equilibrio rotacional cuando puede rotar respecto a un punto fijo al aplicarle una fuerza determinada y a una distancia del punto de rotación. Al efecto de rotación se le denomina TORQUE y se representa con la letra griega τ.

DEFINICIÓN: El Torque τ. o momneto de fuerza, de una fuerza F que actúa sobre algún punto del cuerpo rígido, en una posición r respecto de cualquier origen O y se define algebraicamente con la expresión:

τ = F. d. senα

2. EJEMPLOS DE TORQUE:

Entonces, el torque 𝝉 será proporcional a:
 la magnitud de la fuerza 𝑭
 la distancia 𝒅 entre el punto de aplicación de la fuerza y el punto de giro
 el ángulo 𝜽 de aplicación de la fuerza.

Se usa la convención de que el torque será positivo si el cuerpo gira en sentido anti-horario, mientras que el torque será negativo si el cuerpo gira en sentido horario.

Unidades del torque: Nm (mismas unidades que W, pero significado diferente.)

4.2.2."SEGUNDA CONDICIÓN DE EQUILIBRIO"

Segunda Condición de Equilibrio:

Un cuerpo se encuentra en equilibrio de rotación si el momento resultante de todas las fuerzas que actúan sobre él, respecto de cualquier punto, es nula.

Matemáticamente se expresa así: ∑ T = 0τ τ.τ

Para el caso de fuerzas coplanares, se debe cumplir que la suma aritmética de los momentos relacionados con rotaciones anti-horarias debe ser igual a la suma aritmética de los momentos relacionados con rotaciones horarias.

Podemos afirmar que un cuerpo eta en equilibrio de traslación y de rotación cuando cumple la 1° y la 2° condición de equilibrio.

4. Ejercicios.

A. Calcular el torque o momento de las siguientes fuerzas.

1) F = 12 N y su brazo d = 5m.

2) F = 6,5 N y su brazo d = 8m.

3) F = 25 N y su brazo d = 15m.

4) El momento de una fuerza vale 60 Nm. Si la fuerza mide 4 N, calcular el brazo de la fuerza.

5) El momento de una fuerza vale 125 N. Calcular el valor de la fuerza si su brazo mide 15 m.

B. De acuerdo a la figura, hallemos:

a) los torque que realizan las fuerzas F1, F2 , F3 y el peso w, en el punto o, si sabemos que la barra pesa 5 N: ( m= 0,5 kg) y F3 forma un ángulo de 60°.( F1= 9 N, F2= 8 N, F3 = 5 N )

b) La suma de las fuerzas presentes:

DESARROLLO

a) Hallemos los torques que realizan cada una de las fuerzas, teniendo también en cuenta, el sentido de la rotación:

a) To1 = F1. d1. sen 90° = 9 N . 8 m .1 = 72 Nm
b) To2 = F2 . d2 . sen90° = 8 N . 2 m . 1 = 16 Nm
c) Tow = W . d . sen 90° = 5 N . 3 m = -15 Nm
d) To3 = F3 . d3 . sen 60° = 5 N . 10 m.(0,866) = - 43.3 Nm

b) Hallemos la sumatoria de las fuerzas:

ΣT = T₁ + T₂ + T ₃+ T_W = 72 Nm + 16 Nm + (-5 Nm) +(- 43,3 Nm) =

= 88 Nm +(- 48,3 Nm) = 19,7 Nm

Conclusión: No hay equilibrio rotacional, y la barra queda inclinada haca el lado derecho.

CLASE 6:

5. APLICACIÓN DEL EFECTO ROTACIONAL:

El efecto rotacional o torque se aplica en la construcción de las maquinas simples, entre ellas tenemos: Palancas, Poleas y Planos Inclinados, que se aplican en la infinidad de las maquinas compuestas que tenemos a nuestra disposición. Estas son:

5.1. PALANCAS:

Se define a la palanca como una barra rígida apoyada en un punto sobre la cual se aplica una fuerza pequeña para obtener una gran fuerza en el otro extremo.

Arquímedes (287-212 a.C), un científico de la antigua Grecia, logró explicar el funcionamiento de la palanca, proclamando una famosa frase: "Dadme un punto de apoyo y moveré el mundo".

Arquímedes establece dos principios

1-. "Si se tiene una palanca en cuyos extremos actúan pesos iguales, la palanca se equilibrará colocando el punto de apoyo en el medio de ella."

2-."Un peso se puede descomponer en dos mitades actuando a igual distancia del punto medio de la palanca"

5.2. POLEAS:

Una polea es una máquina simple, un dispositivo mecánico de tracción, que sirve para transmitir una fuerza. Además, formando conjuntos —aparejos o polipastos— sirve para reducir la magnitud de la fuerza necesaria para mover un peso.

Según la definición de Hatón de la Goupillière, «la polea es el punto de apoyo de una cuerda que moviéndose se arrolla sobre ella sin dar una vuelta completa»¹ actuando en uno de sus extremos la resistencia y en otro la potencia.

Las poleas se pueden clasificar de la siguiente manera:

POLEAS SIMPLES: esta clase de poleas se utiliza para levantar una determinada carga. Cuenta con una única rueda, a través de la cual se pasa la soga. Las poleas simples direccionan de la manera más cómoda posible el peso de la carga.

POLEAS FIJAS: consiste en un sistema donde la polea se encuentra sujeta a la viga. De esta manera, su propósito consiste en direccionar de forma distinta la fuerza ejercida, permitiendo la adopción de una posición estratégica para tirar de la cuerda. Las poleas fijas no aportan ninguna ventaja mecánica. Es decir, la fuerza aplicada es igual a la que se tendría que haber empleado para elevar el objeto sin la utilización de la polea.

POLEAS MÓVILES: esta clase de poleas son aquellas que están unidas a la carga y no a la viga, como el caso anterior. Se compone de dos poleas: la primera esta fija al soporte mientras que la segunda se encuentra adherida a la primera a través de una cuerda. Las poleas móviles permiten multiplicar la fuerza ejercida, debido a que el objeto es tolerado por las dos secciones de la soga. De esta manera, la fuerza aplicada se reduce a la mitad. Y la distancia a la que se debe tirar de la cuerda es del doble.

POLEAS COMPUESTAS: el sistema de poleas compuestas se utiliza con el propósito de alcanzar una amplia ventaja de carácter mecánico, levantando objetos de gran peso con un esfuerzo mínimo. Para su ejecución se emplean poleas fijas y móviles. Con la primera se cambia la dirección de la fuerza a realizar. El sistema de poleas móviles más común es el polipasto.

5.3. PLANOS INCLINADOS:

El concepto, por lo general, permite nombrar a la maquinaria simple lograda a partir de un área plana capaz de lograr respecto a la base un ángulo agudo y que se usa para elevar un cuerpo a una determinada altura. Esto ayuda a que se requiera una menor fuerza para levantar el cuerpo que si se tratara de elevarlo de manera vertical.

Como es una máquina simple, funciona como como tal, ya que disminuye el trabajo que se debe realizar cuando se desea cambiar de posición, altura un cuerpo, y en este caso a velocidad constante.

6. ANIMACIONES:

Veamos como funcionan las palancas y las poleas

Así funciona el efecto rotacional, en un balancín:

7. TALLER DE APLICACIÓN 2:

Resolver los siguientes ejercicios

1) Determinar la intensidad de la fuerza F4 según los datos del gráfico.

2) ¿Cuál es la potencia que equilibra una palanca cilíndrica, pesada, homogénea de 3 m de longitud y 25 kgf de peso, si esta apoyada en un punto que dista 90 cm del extremo donde se ha aplicado una resistencia de 350 kgf?

3) Con los datos del croquis, indique a que distancia estará la fuerza F2.

4) Calcular el valor de la potencia aplicada a una palanca, cuyos brazos de potencia y resistencia, son respectivamente, 1,20 m y 30 cm, siendo la resistencia de 80 N, ¿de qué género es la palanca?

5) Un señor emplea una caña de pescar de 2 m de longitud. ¿Qué fuerza aplica para mantener en equilibrio la pieza lograda, si pesa 50 kgf y toma la caña 1,20 m del apoyo?

6) En una palanca de 2° genero, tiene un brazo de potencia Bp = 1,20 m y un brazo de resistencia Br = 0,80 cm. Entonces la multiplicación de la palanca es:

7) Calcular el momento de una fuerza de 125 kgf, respecto de un punto situado a 37 cm. El angulo queforma la fuerza con la horizontal es 37°.

DESARROLLO

El mundo de la fisica por ALONSO

lunes, 22 de agosto de 2016

ESTÁTICA