CINEMÁTICA 1. M.R.U.

LA CINEMÁTICA

Concepto de Cinemática: 

La cinemática es la rama de la mecánica que se ocupa de la descripción del movimiento sin tener en cuenta sus causas. La velocidad (la tasa de variación de la posición) se define como la razón entre el espacio recorrido (desde la posición x₁ hasta la posición x₂) y el tiempo transcurrido.

En la cinemática, se estudia el movimiento de los cuerpos conforme a la trayectoria que describen al desplazarse,  que puede ser rectilínea y curvilínea, incluido el circular, y que para su estudio lo podemos dividir  en cinco movimientos básicos:

1- Movimiento rectilíneo uniforme ( M.R.U.)

2- Movimiento rectilíneo uniformemente acelerado (M.U.A.)

   2.1.- Caída libre

3- Movimiento Parabólico

4- Movimiento Semiparabólico

5- Movimiento circular uniforme (M.C.U.)

1-  MOVIMIENTO RECTILÍNEO UNIFORME

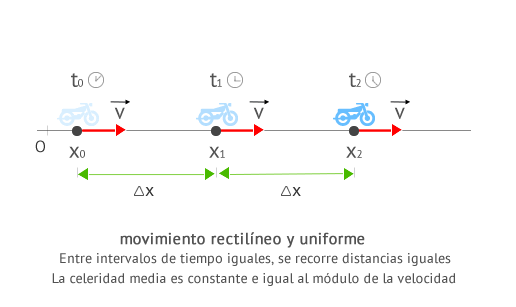
Tambien llamado Movimiento Rectilineo Uniforme, es el movimiento mas sencillo, pues es aquel aquél en el que la velocidad es constante. En el caso más sencillo, la velocidad podría ser nula, y la posición no cambiaría en el intervalo de tiempo considerado. Si la velocidad es constante, la velocidad media (o promedio) es igual a la velocidad en cualquier instante determinado. Si el tiempo t se mide con un reloj que se pone en marcha con t = 0, la distancia x recorrida a velocidad constante  v ,será igual al producto de la velocidad por el tiempo. En el movimiento rectilíneo uniforme la velocidad es constante y la aceleración es nula.

La ecuación que define este movimiento es: x = v . t

Donde: la velocidad v  es   constante, luego su aceleración es a  = 0

VELOCIDAD:  Es la razón o el cociente entre el desplazamiento de un cuerpo y el tiempo trascurrido, y se expresa matemáticamente así:

Ejemplo:

 

Ecuaciones:

La ecuación básica de este movimiento se obtiene de la formula de la velocidad:  v = x / t

Así seria las posibles combinaciones, utilizando el triángulo mágico, así: Donde se puede deducir que:

GRÁFICAS DEL M.R.U:

Las obtenemos de la relación entre: distancia - tiempo y velocidad tiempo, así:

ANÁLISIS:

GRÁFICA 1 :  Relaciona distancia vrs tiempo. Es una linea recta ascendente, por que a mayor distancia, se requiere mayor tiempo. Parte de cero o del reposo.

GRÁFICA 2 : Relaciona velocidad vrs tiempo. Es una linea recta horizontal por que la velocidad es la misma mientras el tiempo trascurre.

GRÁFICA E : Relaciona aceleración vrs tiempo. Es una linea horizontal que vale cero; por que en este movimiento no existe aceleración, por que la velocidad es constante.

VÍDEO:  EL MOVIMIENTO RECTILÍNEO UNIFORME:

Enlace: https://www.youtube.com/watch?v=edaw_kjmxss&t=57s

Ver vídeo: CINEMÁTICA EN 3 D

NOTA:  Si el móvil lleva una distancia inicial diferente de cero, la ecuacion general para el M.R.U., en este caso es:

 

1. Ejemplo de aplicación en la solución de un pequeño problema:

Un niño se mueve en una bicicleta, en linea recta a lo largo de una  calle de su barrio, que tiene un largo de 300 m y lo recorre en un tiempo de  60 segundos.  ¿Cual es la velocidad media de este movimiento?

Rta//  Datos  x = 300 m
                      t = 60 seg


                      v = ?

Aplicamos la formula de la velocidad:  v = x / t
                                            luego :     v = 300 m / 60 seg
                                           entonces   v =  5 m/seg
2. Ejemplo:  Un rayo cae a una distancia de 3.500 de un casa de campo.  Si se sabe que el rayo tiene un efecto sonoro de 340 m/seg.  ¿Que tiempo demoró en caer a tierra, desde el momento  en que se escucha?

Rta//  Datos:  x = 3.500 m
                      v = 340 m/seg
                         t = ?

Aplicamos la expresión para el tiempo  t = x / v 
                                                  luego    t = 3.500 m / 340 m/seg
                                                entonces t = 10,29 seg


TAREA:  Resuelva los siguientes ejercicios: 

Problema 1

Un camión se mueve a velocidad constante de 90 km/h por una autopista recta.

1. ¿qué distancia recorre en 2 horas?
2. ¿qué distancia recorre por segundo?
3. ¿cuánto tardará en recorrer 10 km?

Problema 2

La velocidad de la luz en el vacío es c = 300 000 km/seg. La luz del Sol tarda en llegar a la Tierra 8 minutos y 19 segundos. Calcular la distancia entre el Sol y la Tierra.

Problema 3

Dibujar la gráfica de la distancia recorrida en función del tiempo y la gráfica de la velocidad en función del tiempo del movimiento rectilíneo uniforme de una aeronave ( avión ) que vuela a una velocidad de 1200 km/h.

Problema 4

La siguiente gráfica representa la velocidad (km/h) en función del tiempo para un automóvil. Calcular la distancia que recorre el automóvil sin hacer uso de las ecuaciones del movimiento ya que se trata de un movimiento con velocidad no constante.

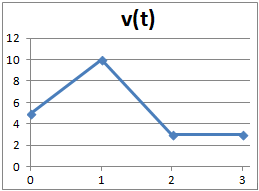
Problema 5

Supongamos  que un cohete espacial recorre 1.200 km a una velocidad constante de 1.500 km/h. Cuando alcanza los 1.200 km, su velocidad pasa a ser, de forma instantánea, 1.900 km/h. A esta velocidad recorre otros 1.200 km. ¿Cual es la velocidad media del cohete cuando hace se recorrido?

DESARROLLO

CASO ESPECIAL:  MOVIMIENTO DE DOS CUERPOS SIMULTÁNEOS

En este tipo de casos puede ocurrir que dos cuerpos se muevan la mismo tiempo en una misma situación y por lo general se pregunte por el tiempo que tardan en encontrarse y las distancias que han recorrido antes del encuentro, muy parecido al problema que plantea el video anterior.

Para estas situaciones se deben plantear las ecuaciones cinemáticas para cada móvil y llevarlas siempre a dos variables, que por lo general son, la distancia y el tiempo; y resolver por cualquiera de los métodos algebraicos.

EJEMPLO:  

Sobre una carretera recta parten dos autos desde dos estaciones de servicio, separadas 125 km. Los autos parten uno contra el otro, al mismo tiempo. Si las velocidades son respectivamente, 65 km/h y 80 km/h.



a) Después de partir los autos, al  cabo de cuanto tiempo se encontraran?
b) Que distancia habrán recorrido cada una?

DESARROLLO:

Datos:  V1 = 65 km/h
              V2 = 80 km/h
               T1 = T2  = T =?  (parten simultáneamente)
              X1 =?
               X2 = ?

Las ecuaciones son:  X1 = V1 . T1
                                     X2 = V2 . T2

Como vamos a hallar el tiempo, igualamos las ecuaciones (por que recorren la misma distancia)
         
                                    T1   =    T2    
                                X1/V1  =  X2 / V2   y como  X2 = 125 - X1
                               X1 / 65 =  ( 125 - X1) / 80

luego:  X1 . 80  =  (125 - X1 ) . 65  =  8.125 - 65 X1

Entonces 80. X1 +  65 . X1  =  8.125

           145 X1   =  8.125

luego  X1 = 8.125 / 145  = 56,03 km

entonces X2 habrá recorrido:  X2 = 125 - 56,03 = 68,97 km

El tiempo empleado en el recorrido será:  T1  =  X1 / V1  =  56,03 / 65 = 0,86 h

lo mismo debe ocurrir con T2 =  X2 / V2  =  68,97 / 80  =  0,86 h

Con base a la anterior explicación, resuelva los siguientes ejercicios:

TAREA 2 :  Resuelva en el cuaderno los siguientes ejercicios de aplicación:


 EJERCICIOS DE M.R.U CON DOS CUERPOS EN MOVIMIENTO


A. Análisis gráfico del MRU:

 a) Interprete y analice la siguiente gráfica.  Calcule la pendiente. 

b) Realice en el cuaderno las gráficas de las siguientes funciones:
     * x = 5.t +10
     * x = 6.t - 4

B. Resuelva los siguientes ejercicios:

2.       Dos trenes parten simultáneamente de una misma estación, con velocidades de 120 km/h y 150 km/h. a que distancia se encuentran uno del otro, al cabo de 3 horas,si

a)      Viajan en la misma dirección.

b)      Viajan en sentido contrario.

3.    Dos autobuses parten simultáneamente de dos terminales, separadas 450 km. Si el primero se mueve a  100 km/h y el segundo a 95 km/h y se mueven uno hacia el otro. ¿Qué tiempo después se encontrarán?

4.    De dos aeropuertos  que distan 6.800 km, parten simultáneamente  dos aviones con velocidades de 420 km/h y 380 km/h, el uno hacia el otro. ¿Al cabo de cuánto tiempo se encuentran  visualmente, y qué distancia habrán recorrido cada uno?

5.    De dos ciudades A y B, que distan 600 km, parten dos autos, el uno hacia el otro, con velocidades de 70 km/h y 95 km/h. Si el auto que parte de B, sale una hora antes, ¿al cabo de cuánto tiempo se encuentran?

6.     Un barco mercante, parte del puerto de Lisboa, hacia la Abana, Cuba, en línea recta y a una velocidad constante de 120 km/h.  Dos horas después de la Abana, parte otro barco mercante, hacia Lisboa, en línea recta y a 150 km/h. ¿En el punto de encuentro, de los dos barcos, que distancia abra recorrido cada barco? (La distancia media entre la Abana y Lisboa e 7.011 km aproximadamente).

7.   El auto de nos asaltantes, parte del banco donde realizaron un asalto a una velocidad de 85 km/h, en línea recta por una autopista. 5 minutos después del suceso, un policía de tránsito, los persigue en su motocicleta a una velocidad 125 km/h.

a)      En el momento de la persecución, ¿qué distancia de ventaja le llevan los ladrones al policía?

b)      ¿Cuánto tiempo, tarda el policía para alcanzar el auto?

c)        ¿Qué distancia habrán recorrido tanto los ladrones como el policía?

                                                        DESARROLLO