MOVIMIENTO CIRCULAR UNIFORME

CINEMÁTICA 4

MOVIMIENTO CIRCULAR UNIFORME (M.C.U)

1. CONCEPTO:  El movimiento circular uniforme describe el movimiento de un cuerpo con una rapidez constante y una trayectoria circular. Aunque la rapidez del objeto y la magnitud de su velocidad son constantes, en cada instante cambia de dirección.

2. EJEMPLOS DE MOVIMIENTO CIRCULAR UNIFORME

1. El movimiento de una rueda de bicicleta

2. El movimiento de las aspas de un ventilador

3. La trayectoria que describe un cuerpo que gira atado a una cuerda

4. El movimiento de una rueda de Chicago o de un Tio -Vivo

3. CONCEPTOS ASOCIADOS AL M.C.U :

Ver video explicativo:   Movimiento Circular Uniforme

PERIODO: El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Se define como:

${\displaystyle T={\frac {2\pi }{\omega }}}$

FRECUENCIA: La frecuencia es la inversa del período, es decir, las vueltas que da un móvil por unidad de tiempo. Se mide en hercios o s^-1

${\displaystyle f={\frac {1}{T}}={\frac {\omega }{2\pi }}}$

VELOCIDAD ANGULAR: es la variación del desplazamiento angular por unidad de tiempo (omega minúscula, ).

En un movimiento circular uniforme, dado que una revolución completa representa 2π radianes, tenemos:

${\displaystyle \omega ={\frac {2\pi }{T}}=2\pi f}$

CONCEPTO DE RADIAN: 

El radián mide el ángulo presentado como central a una circunferencia y su medida es igual a la razón entre la longitud del arco que comprende de dicha circunferencia y la longitud del radio, es decir, mide la cantidad de veces que la longitud del radio cabe en dicho arco.

VELOCIDAD LINEAL O TANGENCIAL: 

•  Es la velocidad del objeto en un instante de tiempo (magnitud vectorial con módulo, dirección y sentido determinados en ese instante estudiado). Puede calcularse a partir de la velocidad angular. Si ${\displaystyle v_{t}}$ es el módulo de la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:

${\displaystyle v_{t}=\omega \,R}$

ACELERACIÓN CENTRÍPETA:

La aceleración centrípeta, también llamada normal o radial, afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. Se define como:

${\displaystyle a_{c}=a_{n}={\frac {v_{t}^{2}}{R}}=\omega ^{2}R}$

4. CARACTERISTICAS DEL MOVIMIENTO CIRCULAR UNIFORME:

1. La velocidad angular es constante (ω = cte)
2. El vector velocidad es tangente en cada punto a la trayectoria y su sentido es el del movimiento. Esto implica que el movimiento cuenta con aceleración normal
3. Tanto la aceleración angular (α) como la aceleración tangencial (at) son nulas, ya que la rapidez o celeridad (módulo del vector velocidad) es constante
4. Existe un periodo (T), que es el tiempo que el cuerpo emplea en dar una vuelta completa. Esto implica que las características del movimiento son las mismas cada T segundos. La expresión para el cálculo del periodo es T=2π/ω y es sólo válida en el caso de los movimientos circulares uniformes (m.c.u.)
5. Existe una frecuencia (f), que es el número de vueltas que da el cuerpo en un segundo. Su valor es el inverso del periodo

5. EJEMPLO DE APLICACION:

Un cuerpo da tres vueltas sobre una circunferencia de 300 metros de diámetro a velocidad constante y tarda 2 minutos en hacerlo.

Calcular:

• Frecuencia
• Período
• Velocidad angular
• Velocidad tangencial
• Aceleración centrípeta

Solución: Paso a paso:

a. Convertimos las el tiempo a segundos.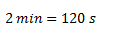



b. Calculamos la frecuencia a través de su definición.



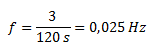
c. Calculamos el período como la inversa de la frecuencia.



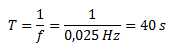
d. Obtenemos la velocidad angular a partir de la frecuencia.



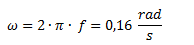
También podríamos haber obtenido esta velocidad en base a su definición, es decir la variación de ángulo sobre la variación de tiempo sabiendo que recorre 3 vueltas (6 π radianes) en 120 segundos.

e. Calculamos la velocidad tangencial multiplicando la velocidad angular (en radianes) por el radio.


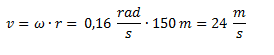
Otra manera de haberla calculado es a través de su definición, es decir haciendo el cociente entre el espacio recorrido y el tiempo empleado, sabiendo que recorrió el perímetro de la circunferencia tres veces en 120 segundos.

f. Por último hallamos la aceleración centrípeta.

6. EJERCICOS DE REFUERZO:

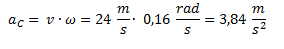
Resuelva los siguientes ejercicios:

Problema n° 1)

1. ¿Cuál es la velocidad angular de un punto dotado de M.C.U. si su período es de 1,4 s?
2. ¿Cuál es la velocidad tangencial si el radio es de 80 cm?

Respuesta: a) 4,48/s; b) 358,4 cm/s

Problema n° 2) Si un motor cumple 8.000 RPM, determinar:

1. ¿Cuál es su velocidad angular?
2. ¿Cuál es su período?

Respuesta: a) 837,76/s; b) 0,007 s

Problema n° 3) Un móvil dotado de M.C.U. da 280 vueltas en 20 minutos, si la circunferencia que describe es de 80 cm de radio, hallar:

1. ¿Cuál es su velocidad angular?
2. ¿Cuál es su velocidad tangencial?
3. ¿Cuál es la aceleración centrípeta?

Respuesta: a) 1,47/s; b) 117,29 cm/s; c) 171,95 cm/s²

Problema n° 4) Un que cuerpo pesa 0,5 N y está atado al extremo de una cuerda de 1,5 m, da 40 vueltas por minuto. Calcular la fuerza ejercida sobre la cuerda.

Respuesta: 1,34 N

Problema n° 5) Calcular la velocidad tangencial de un volante que cumple 3.000 RPM si su radio es de 0,8 m.

Respuesta: 251,3 m/s

Problema n° 6) Un volante de 20 cm de radio posee una velocidad tangencial de 22,3 m/s. Hallar:

1. ¿Cuál es su frecuencia?
2. ¿Cuál es su número de RPM?

Problema n° 7) La velocidad tangencial de un punto material situado a 0,6 m del centro de giro es de 15 m/s. Hallar:

1. ¿Cuál es su velocidad angular?
2. ¿Cuál es su período?

Problema n° 8) Una polea cumple 2.000 RPM, calcular la velocidad angular en grados sobre segundo.

Respuesta: 12.000 grad/s

Problema n° 9) Calcular la velocidad angular de un volante que da 2.000 RPM

Respuesta: 209,4/s